Backtracking ist eine mit der Rekursion verwandte Problemlösungsstrategie.
Beim Backtracking probiert man jede mögliche Lösung aus, überprüft allerdings mit jedem Schritt die Abbruchbedingungen des Problems. Ist eine der Abbruchbedingungen gegeben, wird dieser “Pfad” nicht weiter verfolgt. Dabei ist der Algorithmus immer sehr ähnlich aufgebaut:
Pseudocode
backtrack()
WENN Problem gelöst
GIB Lösung ZURÜCK
Finde Element im Ursprungszustand
DURCHLAUFE jeden Zustand
WENN Zustand zulässig
Setze Zustand um
WENN backtrack() Lösung findet
GIB Lösung ZURÜCK
Mache Zustand Rückgängig
GIB keine Lösung ZURÜCK
Für jedes Element des Problems (Spalten im Damenproblem, Länder im Vierfarbenproblem…) werden alle möglichen Zustände ausprobiert (Z. 5f). Ist ein Zustand zulässig (Z. 7), so wird diese Möglichkeit umgesetzt (Z. 8) und rekursiv überprüft, ob es eine Lösung für den aktuellen Zustand gibt (Z. 10). Gibt es diesen, wird er zurückgegeben (Z. 11). Gibt es diesen nicht, wird der vorherige Schritt rückgängig gemacht (Z. 13) und der nächste Zustand überprüft. Sollten alle möglichen Zustände überprüft worden sein, ohne dass eine Lösung gefunden wurde, dann gibt es für den aktuellen Zustand keine Lösung und das wird dementsprechend zurückgegeben (Z. 15).
Die Rekursionsbasis stellt der Fall ein, dass das Problem gelöst ist: Dann wird einfach die Lösung zurückgegeben (Z. 2f).
Bedingungen an das Problem
Damit ein Problem effizient per Backtracking gelöst werden kann, muss es folgende Eigenschaften besitzen:
- Das Problem ist in endlich vielen Teilschritten lösbar
- Jeder der Teilschritte besitzt Abbruchbedingungen
- Jeder der Schritte hat eine endliche Anzahl Lösungsmöglichkeiten
Ein Problem muss nicht zwingend eine Lösung besitzen, um effizient mit Backtracking gelöst zu werden. Ein unlösbares Problems wird als solches erkannt.
Am Beispiel des Vierfarbenproblems
Beim Vierfarbenproblem geht es darum, eine Karte mit Ländern unter Verwendung von Farben einzufärben.
Dabei müssen für jedes Feld zwei Bedingungen erfüllt sein:
Das neu gefärbte Land grenzt an kein bereits früher gefärbtes Land mit der gleichen Farbe.
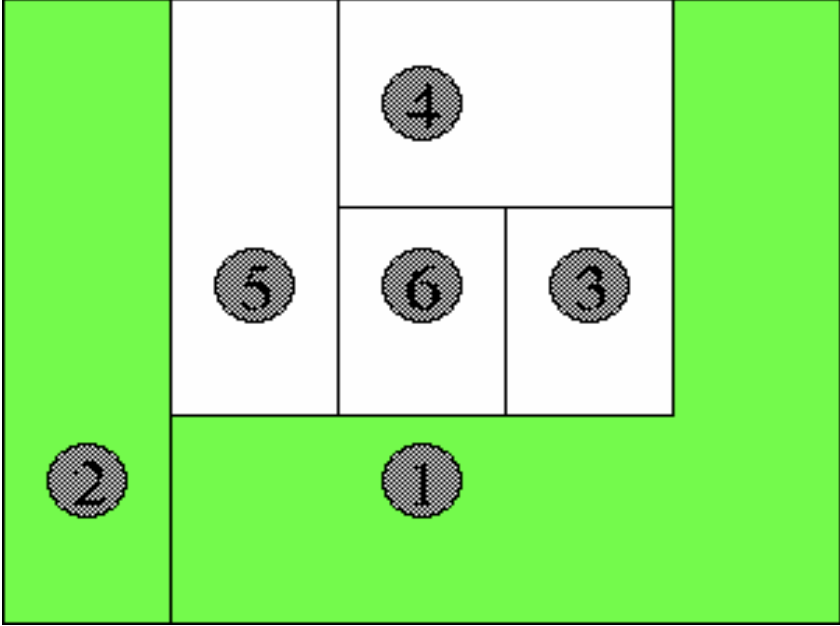
Durch die Färbung des neuen Landes wird kein angrenzendes, noch nicht gefärbtes Land unfärbbar.
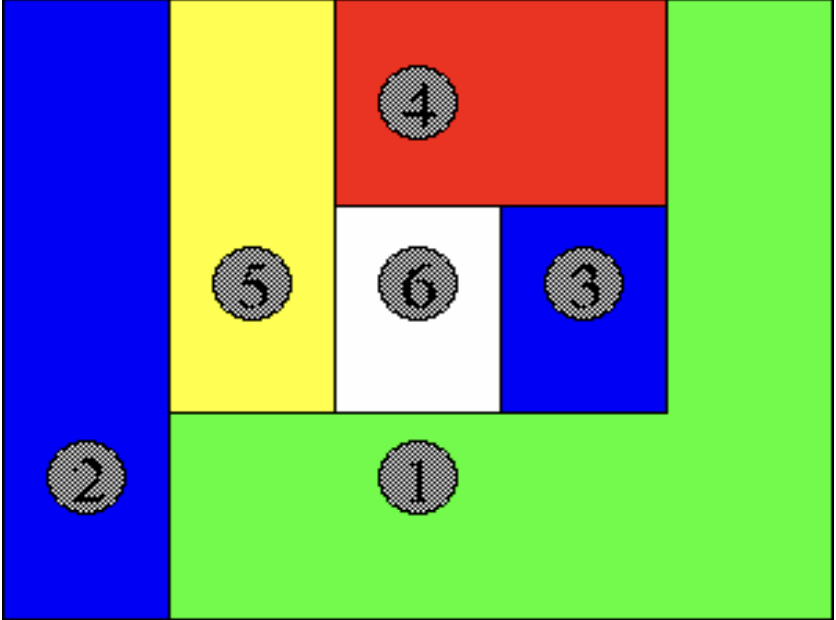
Die Bilder zeigen jeweils Fälle, in denen die Bedingungen nicht erfüllt sind.
Die Zweite Bedingung ist nicht zwingend notwendig, macht die Problemlösung allerdings deutlich einfacher.
Pseudocode
Zu Demonstrationszwecken ist der folgende Code auf Felder ausgelegt. Wir stellen erstmal den Pseudocode für unsere beiden Bedingungen auf:
bedingung1(i, farbe)
FÜR alle angrenzenden
WENN Farbe des angrenzenden gleich farbe
GIB false ZURÜCK
GIB true ZURÜCK
Um herauszufinden, ob man eine Farbe setzen kann, überprüft man jedes der angrenzenden Länder.
bedingung2(i)
ERZEUGE Liste
FÜR alle angrenzenden
HÄNGE Farbe AN Liste AN
FALLS Liste enthält Blau UND
Liste enthält Gelb UND
Liste enthält Grün UND
Liste enthält Rot
GIB false ZURÜCK
SONST
GIBT true ZURÜCK
Wir tragen die Farbe aller umliegenden Felder in eine Liste ein. Wenn diese Liste alle Farben enthält (im Beispiel Blau, Gelb, Rot und Grün), ist die Bedingung nicht erfüllt.
Um nun das Problem zu lösen, benutzen wir folgenden Algorithmus:
vierFarbenProblem()
FALLS alle Felder eingefärbt sind
GIB Farben der Felder ZURÜCK
finde das erste Land ohne Farbe
DURCHLAUFE ALLE farben
FALLS
bedingung1(land, farbe) UND
bedingung2(land)
DANN
SETZE farbe
FALLS vierFarbenProblem() eine Lösung zurückgibt
GIB die Lösung zurück
SETZE farbe zurück
GIB keine Lösung zurück
In Zeile 2f. ist die erste Rekursionsbasis: Sie überprüft, ob das Problem gelöst wurde. Wenn es gelöst wurde, wird die Lösung zurückgegeben.
Greift die Rekursionsbasis nicht, gehen wir in den Schritt über:
Wir finden ein Land ohne Farbe (Z. 5) und iterieren über alle Lösungsmöglichkeiten (in unserem Fall Farben ).
Falls diese Farbe beiden Bedingungen genügt, wird sie “ausprobiert”:
Die Farbe wird erst gesetzt (Z. 11).
Dann wird überprüft, ob es für diese Konstellation eine Lösung gibt (Z. 12).
Gibt es diese, wird sie zurückgegeben (Z. 13), sonst wird das Setzen der Farbe wieder rückgängig gemacht (Z. 14) und in der nächsten Iteration die nächste Farbe ausprobiert.
Falls über alle Farben iteriert wurde, ohne eine Lösung zu finden, gibt es für diesen Zustand keine Lösung und “keine Lösung” wird zurückgegeben (Z. 15).
Demonstration
In diesem Beispiel stellt jeder Knoten ein Land dar, jede Kante die gemeinsame Grenze mit einem anderen. Mit den Preset-Tasten wählt man eine Voreinstellung an, mit dem Backtrack-Taster startet man den Algorithmus. Bleiben die Felder Grau, ist keine Lösung möglich.
Das ganze ist mithilfe der Visualisierungs-Biblothek Vis.js entstanden, die zentrale Methode sieht so aus:
const backtrack = () => {
// Basis 1: Lösung gefunden
if (allColored()) return data;
const betrachtet = getFirstUncolored();
for (let color of FARBEN) {
if (
bedingung1(
betrachtet,
color
) &&
bedingung2(betrachtet)
) {
setColor(betrachtet, color);
const solution = backtrack();
if (solution !== null) return solution;
setColor(betrachtet, FARBLOS);
}
}
return null
};
Präsentation
Das Vierfarbenproblem als Präsentation
Am Beispiel von Sudoku
Sudoku ist ein beliebtes Zahlenrätsel, bei dem es um das ausfüllen eines Zahlenfeldes nach bestimmten Regeln geht.
Eine Matrix der Dimension (selten andere Größen) besteht aus Submatrizen der Dimension . Jede Komponente sei eine natürliche Zahl , sodass in jeder Spalte, Zeile und Submatriz einzigartig ist.
Dabei sind zu Beginn schon einige Zahlen eingetragen.

Zur Lösung eines Sudokus kann man sehr gut Backtracking verwenden. Dabei sind die Komponenten unsere Elemente und die Zahlen die möglichen Zustände dieser.
Pseudocode
WENN Alle Komponenten befüllt
GIB Feld ZURÜCK
Finde leere Komponente
DURCHLAUFE 1..9
WENN Zahl zulässig
Setze Zahl
WENN backtrack() Lösung findet
GIB Lösung ZURÜCK
Entferne Zahl
GIB keine Lösung ZURÜCK
